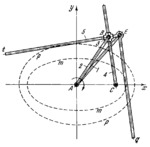
The lengths of the links comply with the conditions: A͞B=a₂ and A͞E=sqrt(a₁²+b₂²)=sqrt(a₂²+b₁²) where a₁ and b₁ are the semiaxes of ellipse m-m, and a₂ and b₂ are the semiaxes of ellipse p-p. Angle tEq equals 90° . Link 1, rotating about fixed axis A, is connected by turning pair E to link 5 which has the form of bent lever tEq. Link 4, rotating about fixed axis C, is connected by a sliding pair to cross-shaped slider 3 which has guides wi th axes perpendicular to each other. Arm Et of link 5 moves in slider 3. Link 2, rotat ing about axis A, is connected by turning pair B to slider 3. Point A is placed at the common centre of ellipses m-m and p-p, and point C at one of their common foci. Then, when link 1 rotates, the arms of the right angle tEq of link 5 simultaneously envelop the confocal ellipses m-m and p-p.
$1051$LG,Ge$