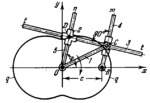
The lengths of the links comply wi th the conditions: 0͞C=a, 0͞B=c=sqrt(a²-b²) and a>c, where a and b are the semiaxes of the ellipse. Link 1 turns about fixed axis 0 and is connected by turning pair C to slider 3. Slider 3 moves along axis Bm of link 4 which turns about fixed axis B. Cross-piece t-t of slider 3 is connected by a sliding pair to cross-shaped slider 2 which has guides perpendicular to each other. Slider 2 moves along axis On of link 5 which rotates about axis 0. Centre 0 is placed at the centre of the ellipse and centre B at one of its foci. Then, when link 1 turns about axis 0, point D of slider 2 describes pedal curve q-q of the ellipse. The equation of the pedal curve is ρD=0͞D=sqrt(a²-c²*sin²(ϕ)) or (x²+y²)²=a²x²+b²y² where ϕ is the polar angle between vector ρD and polar axis 0x.
$1166$LG,Ge$