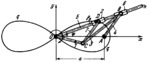
The lengths of the links comply with the conditions: 0͞A=B͞C=a, 0͞C=A͞B=C͞D=b and b<a. Figure OABC is a crossed-crank linkage. Link 1 turns about fixed axis 0 and is connected by turning pairs C to links 3 and 7 . Links 3 and 7 are connected by turning pairs B and D to sliders 6 and 2 which move along axis On of link 5. Link 5 turns about fixed axis 0. When link 1 turns about axis 0 , point D of slider 2 describes hyperbolic lemniscate of Bouth q-q with the equation ρD=0͞D=2sqrt(b²-a²*sin²(ϕ)) or (x²+y²)²=d²x²-f²y² where d²=4b², f²=4(b²-a²), ϕ = polar angle between vector ρD and polar axis 0x. If the lengths of the links also comply with the condition a=c*sqrt(2), then point D describes a lemniscate of Bernoulli.
$1179$LG,Ge$