 Ansicht vergrößern Ansicht vergrößern
|
Beschreibung
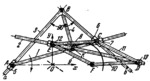
The lengths of the links comply with the conditions: E͞C=C͞D=D͞F=F͞E, i.e. figure ECDF is a rhombus linkage. Arm Ba of bent link 3 moves in slider 5 which turns about fixed axis A. Arm Bb of link 3 moves in slider 6 which is connected by turning pair C to slider 7. Link 4 is connected by turning pair B to link 3 and by a sliding pair to link 1. The axis of link 4 is perpendicular to that of link 1. Links 8, 9, 10 and 11 are connected together by turning pairs E, F, D and C. Links 9 and 10 turn about fixed axis F. Link 2 is connected by turning pair K to link 4 and by sliding pairs to sliders 12 and 13, constituting diagonal ED of paral lelogram ECDF. When link 1 turns about axis A, point K of link 4 describes a Cassinian oval with the equation (with respect to the origin of coordinates 0) (x²+y²)-2d²(x²-y²)=a⁴-d⁴ where a=B͞K, 2d=A͞F=20͞F=20͞A.
$1198$LG,Ge$
|

 Ansicht vergrößern
Ansicht vergrößern






