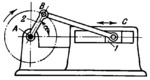
The axis of slider 1 passes through the axis of rotation of crank 2. Displacement s of the slider from its right-hand extreme (dead- centre) position is s=A͞B(1-cos(α))+B͞C(1-sqrt(1-(A͞B/B͞C)²cos(2α))) where α is the angle of rotation of the crank. If ratio is A͞B/B͞C sufficiently low then the approximate equation s=r[(1+(1/4)(A͞B/B͞C))-(cos(α)+(A͞B/B͞C)cos(2α))] where r=A͞B, can be used. The velocity of point C can be determined by the equation v_c=v_b(sin(α)+(((A͞B/B͞C)sin(α)cos(α))/(sqrt(1-(A͞B/B͞C)²sin²(α))))) v_c=v_b(sin(α)+1/2(A͞B/B͞C)sin(α))
where v_b is the velocity of point B of crank 2. The full stroke of slider 1 equals S=2A͞B.
$1477$SC,4L$