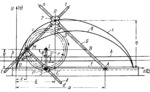
Gear 3 meshes with fixed gear rack 1 and is connected by turning pair L to cross-shaped slider 2 which moves along fixed guides b-b. Slider 2 is connected by turning pair P to slider 5 which moves along axis Md of T-shaped link 4. Link 4 is connected by turning pair M to gear 3 and its crosspiece t-t moves in cross-shaped slider 7 which has guides perpendicular to each other. Slider 7 moves along axis An of link 6 which turns about fixed axis A located on axis Ox at the arbitrary distance O͞A=a. The dimensions of the links comply with the condition: M͞L=L͞P=r, where r is the pitch radius of gear 3. When slider 2 travels with translational motion along guides b-b, gear 3 rolls along rack 1 and point M describes cycloid q of a circle of radius r, with the parametric equations x=rθ-r sin(θ) and y=r-r cos(θ). Point D of slider 7 describes pedal curve s-s of cycloid q with its centre at point A. The parametric equations of the pedal curve are η=r(1-cos(θ))+((a-rθ)/2)sin(θ)and ξ=a-r sin(θ)-((a-rθ)/2)(1+cos(θ)) where θ is angle MLP.
$2475$LrG,Ge$