 Ansicht vergrößern Ansicht vergrößern
|
Description
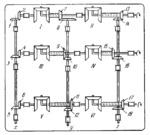
The mechanism can solve a system of three equations with three unknowns: x+a₁y+b₁z=c₁, x+a₂y+b₂z=c₂, x+a₃y+b₃z=c₃ where a, b and c are given constants. The bevel gear pairs 1 and 2, 3 and 4, and 5 and 6 have a transmission ratio equal to unity. The transmission ratios of bevel gear pairs 7 and 8, 9 and 10, and 11 and 12 are i₇,₈=a₁, i₉,₁₀=a₂ and i₁₁,₁₂=a₃. The transmission ratios of bevel gear pairs 13 and 14, 15 and 16, and 17 and 18 are i₁₃,₁₄=0,5b₁, i₁₅,₁₆=0,5b₂ and i₁₇,₁₈=0.5b₃. Owing to the properties of a bevel gear differential, the carrier of differential II turns an amount equal to one-fourth of the left side of the first equation, the carrier of differential IV an amount equal to one-fourth of the left side of the second equation and the carrier of differential VI an amount equal to one-fourth of the left side of the third equation. The angles of rotation of shafts x, y and z are proportional to the values of the unknowns.
$2950$CxG,MO$
|

 Ansicht vergrößern
Ansicht vergrößern






