 Ansicht vergrößern Ansicht vergrößern
|
Beschreibung
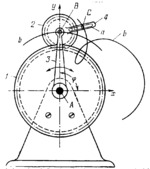
Carrier 3 rotates about fixed axis A and is connected by turning pair B to planet gear 2 which meshes with fixed sun gear 1. Planet gear 2 has integral lever 4 with straight slot a. Adjustable along slot a is stylus C which can be secured at a variable distance B͞C from axis B and which describes epicycloid b-b with the equation x=(R+r)cos(ϕ)-λrcos(((R+r)/r)ϕ); y=(R+r)sin(ϕ)-λrsin(((R+r)/R)ϕ) where R is the pitch radius of sun gear 1, r is the pitch radius of planet gear 2, λ=B͞C/r, B͞C is the distance from axis B to tracing point C, and ϕ is the angle of rotation of carrier 3. As shown, λ=B͞C/r>1 and therefore curve b-b is a prolate epicycloid. At λ=B͞C/r<1, point C describes a curtate epicycloid. If λ=1, then point C is on the pitch circle of planet gear 2 and describes an epicycloid. When m=R/r is a whole number the epicycloid consists of m identical noncrossing branches. If m is fractional, the epicycloid crosses to form loops.
$2380$SG,Ge$
|

 Ansicht vergrößern
Ansicht vergrößern






