
|
DMG-Lib Home + News
|
Browse
|
Search
|
Experience DMG-Lib
|
About us
|
Help
|
|
|
|||||||
ARTOBOLEVSKY LINK-GEAR MECHANISM FOR CONVERTING CIRCLES INTO PIRIFORM CURVES |
|||||||
|---|---|---|---|---|---|---|---|
 Click to enlarge Click to enlarge
|
Description
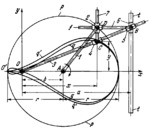
The lengths of the links comply with the condition: A͞D=r, where r is the radius of circle p-p which is to be converted into a piriform curve. Link 1 turns about fixed axis A and is connected by turning pair D to cross-shaped slider 2 which has guides perpendicular to each other. Link 3 turns about fixed axis 0 and is connected by sliding pairs to sliders 4 and 5. Slider 5 is connected by turning pair B to slider 6 which moves along fixed guides t-t whose axis is parallel to axis 0y. Cross-piece Bf of slider 6 has its axis parallel to axis 0x and is connected by a sliding pair to slider 2. Link 7 is connected by turning pair C to slider 4 and by a sliding pair to slider 2. When link 1 turns about axis A, point D describes circle p-p, and point C of slider 4 describes generalized piriform curve q-q with the equation x⁴-2bx³-(r²-b²)x²+ay²=0 where a and b are constant dimensions of the mechanism. If the axis about which link 3 turns is moved to point 0', located on the circle, then point C describes piriform curve q'-q' with the equation x⁴-2rx³+a²y²=0. |
||||||
| Linked items | |||||||
|
|||||||
| Permanent links | |||||||
|
|
|||||||
| Data provider | |||||||
|
|
|||||||