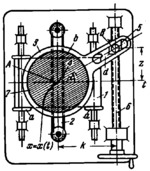
This instrument is intended for the graphic differentiation of various curves of the type x=x(t), i.e. to obtain the value of the function x=x(t). Curve x=x(t) is plotted on paper tape 1 which is wound from one reel a to the other at a rate proportional to the quantity t. Pencil 4 is secured to flexible cord 2 and is displaced vertically at a rate proportional to quantity x. Thus, in simultaneous motion of paper tape 1 and pencil 4, the continuous curve x=x(t) is traced on the tape. Link 3, turning about fixed axis A, has slot d which slides along pin B of nut 5. Nut 5 is connected by a screw pair to screw 6. Transparent disk 7, secured rigidly to link 3, has on its face engiraved lines b parallel to the axis of slot d. To find the derivat ve of function x=x(t), disk 7 and link 3 are swivelled by turning screw 6 until one of the lines b is tangent to the curve x=x(t) at the point at which the derivative x=x(t) is to be found. The quantity proportional to this derivative is tan(α)=(1/k)z where α = angle between line AB and axis At, k = constant dimension of the mechanism, being the distance from point A to the axis of screw 6.
$1299$LG,MO$