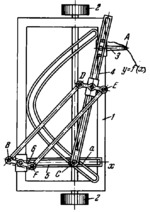
When stylus A is moved along curve y=f(x), carriage 1 travels on rollers 2 along the x-axis. Slider 3 moves along the right- hand guide of carriage 1 and slotted link 4 turns about pivot C which slides2 along guide a of parabolic shape with the equation x=1-y². At this, pin C moves slotted link 5 along the left- hand guide of carriage 1. By means of parallel-crank linkage BDEF, whose side DE is perpendicular to slotted link 4, the plane of wheel 6 (shown with dash lines) is always perpendicular to link 4. If guide a is of parabolic shape the mechanism can integrate the equation (dv/dx)=(v(sin(α))+Ψ(v))/cos(α) where v = velocity of the shell, α = angle of inclination of the trajectory to the horizon, Ψ(v) = velocity function (resistance of the medium divided by the acceleration of gravity). Substituting v=e^x and y=sin(α), we obtain dy/dx=-(1-y²)/(f(x)-y) where f(x)=Ψ(e^x).
$1315$LG,MO$