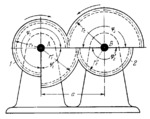
Gears 1 and 2 rotate about fixed axes A and B. Each gear is composed of two gear segments with the pitch radii r₁, r₁', r₂ and r₂'. Taking the sign of the angular velocities into account, the transmission ratio of the mechanism changes twice each cycle and equals i₁₂=ω₁/ω₂=-r₂/r₁=-z₂/z₁ and i₁₂'=ω₁'/ω₂'=-r₂'/r₁'=-z₂'/z₁' where ω₁, ω₁', ω₂ and ω₂' are the angular velocities of gears 1 and 2, and z₁, z₁', z₂ and z₂' are the numbers of teeth of full gears having the same pitch radii as the corresponding gear segments. The pitch radii of the gear segments are related to their central angles ϕ₁, ϕ₁'=2π-ϕ₁, ϕ₂ and ϕ₂'=2π-ϕ₂ by the conditions: r₁=(aϕ₂)/(ϕ₁+ϕ₂), r₁'=(aϕ₂')/(ϕ₁'+ϕ₂'), r₂=(aϕ₁)/(ϕ₁+ϕ₂), r₂'=(aϕ₁')/(ϕ₁'+ϕ₂') where a is the centre-to-centre distance. For the given mechanism ϕ₁=3ϕ₁' and ϕ₂=ϕ₂'. Therefore, r₁=0.4a, r₂=0.6a, r₁'=0.67a and r₂'=0.33a. Impacts at the instants of transition from the engagement of one pair of gear segments to that of the other pair are avoided by the provision of supplementary conjugate cam surfaces having profiles with special curves.
$2314$SG,3L$