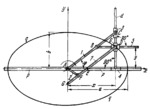
The lengths of the links comply with the conditions: F͞E=(a+b)/2, A͞F=(a-b)/2 and G͞F=F͞E=A͞F, where a and b are the semiaxes of the ellipse. Link 1, rotating about fixed axis A, is connected by turning pairs B and C to link 5 and slider 3 which moves along bar d of slider 4. Link 5 moves in cross- shaped slider 6 which has guides with axes perpendicular to each other. Slider 6 moves along bar d of slider 4 which, in turn, moves along fixed guides p-p. When link 1 rotates, point D of slider 6 describes ellipse q-q whose parametric equations are x=a*cos(ϕ) and y=b*sin(ϕ) where ϕ is the angle between axis A͞C of link 1 and axis Ax of guides p-p. If to this basic mechanism one adds link 2, rotating about fixed axis A, and link 7, connected by turning pairs F and D to link 2 and slider 6, then points E and G of link 7 move along axes Ax and Ay, and therefore any point of link 7 describes an ellipse.
$1049$LG,Ge$