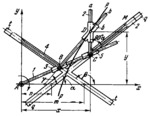
Link 1, turning about fixed axis A, is connected by sliding pairs to sliders 3 and 5. Slider 3 is connected by turning pair B to slider 4 which moves along fixed guides t-t. The axis of guides t-t makes the angle β with axis Ax. Cross-piece Bb of slider 4 is connected by a sliding pair to X-shaped slider 6 which has guides making the angle 90°-γ with each other, where γ is the angle made by cross-piece Bb wi th axis Ax. Slider 2 moves along fixed guides q-q whose axis makes the angle a with axis Ax. Cross-piece Ca of slider 2 moves in slider 6. When link 1 turns about axis A, point D of slider 6, at the intersection of lines Bb and Ca, describes hyperbola p-p with the equation ex²+fxy+2gx+2hy+j=0 where e=(tan(β)-tan(α))tan(β), f=-(tan(β)-tan(α)), g=-(m*tan(β)tan(γ)-n*tan(α)tan(γ)-m*tan(α)tan(β))/2, h=-n*tan(α), j=-mn*tan(α)tan(β), m and n = constant dimensions of the mechanism.
$1082$LG,Ge$