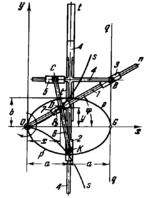
The lengths of the links comply with the conditions: D͞K=a and D͞C=b, where a and b are the semiaxes of ellipse p-p. Link 1, turning about fixed axis 0, is connected by sliding pairs to sliders 7 and 3. Cross-shaped slider 4 moves along fixed guides t-t whose axis is perpendicular to axis 0x. Cross-piece CB of slider 4 is connected by a sliding pair to slider 5 and by turning pair B to slider 3. Link 6 is connected by turning pairs C, D and K to sliders 5, 7, and 2. Slider 2 is connected by a sliding pair to slider 4. When link 1 turns about axis 0, point D of link 6 describes cissoid s-s of ellipse p-p and of straight line q-q tangent to this ellipse at point G. The equation of curve s-s is ρD=0͞D=2a/cos(ϕ)-2(b²/a)cos(ϕ)/(sind²(ϕ)+(b²/a²)*cos²(ϕ)) or y²=(b²/a²)*(x³/(2a-x)) where ϕ is the polar angle between vector ρD and polar axis 0x.
$1133$LG,Ge$