 Cliquez pour agrandir Cliquez pour agrandir
|
Description
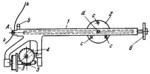
When stylus A is moved along curve k, link 1 of the integrator slides along pin d of fixed disk 2 and turns through a certain angle φ. The number of revolutions of measuring wheel 3 is found from the equation n=(1/(2πa))∫(r)dφ; with limits [0,φ] where a = radius of measuring wheel 3, r = distance from stylus A to the axis of pin d, axis being the origin of coordinates. Since the mean radius of curvature of curve k is r_m=(1/φ)∫(r)dφ; with limits [0,φ] then r_m=(2π/φ)an where r is the instantaneous radius of curve k. When stylus A is traced around a closed curve, r_m=an. Dial 4 driven by measuring wheel 3 through worm 5 and a worm wheel rigidly secured to dial 4, indicates the whole revolutions of wheel 3, and the circular scale on the wheel indicates the fraction of a revolution. Pin b, needle points c of disk 2 and roller 6 serve as supports for the integrator.
$1308$LG,MO$
|

 Cliquez pour agrandir
Cliquez pour agrandir






