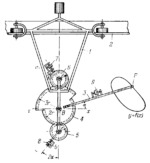
When tracing point F is moved along curve y=f(x), carriage 1 travels along guide 2 parallel to axis x-x and gear 4, rigidly attached to lever 3, turns about axis B of carriage 1. Gear 4 consists of two segments of pitch radii 2r and 3r, where r is the pitch radius of gears 5 and 6. Rotation of gear 4 is transmitted to gears 5 and 6 to which the frames b and a of recording wheels 8 and 7 are rigidly attached. Angle ϕ₉ of rotation of recording wheel 9, whose frame is mounted on lever 3, is proportional to the area A of the closed curve. Thus ϕ₉=k∫ydx=kA; with limits [x₁,x₂]. Angle ϕ₈ of rotation of wheel 8 is proportional to the static moment of area A with respect to axis x-x: ϕ₈=k∫(sin(π/2-2α))dx=k∫y²dx; with limits [x₁,x₂], [x₁,x₂]. Angle ϕ₇ of rotation of wheel 7 is proportional to the moment of inertia of area A with respect to axis x-x: ϕ₇=k∫(sin(3α))dx=k∫(y³)dx; with limits [x₁,x₂], [x₁,x₂].
$2505$LrG,MO$