 Click pentru a mări Click pentru a mări
|
Description
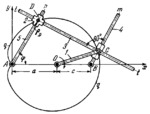
The lengths of the links comply with the conditions: 0͞C=0͞A=a, 0͞B=c=sqrt(a²+b²) and a>c, where a and b are the semiaxes of the ellipse. Link 1 turns about fixed axis 0 and is connected by turning pair C to slider 3. Slider 3 moves along axis Bm of link 4 which turns about fixed axis B. Crosspiece t-t of slider 3 is connected by a sliding pair to cross-shaped slider 2 which has guides perpendicular to each other. Slider 2 moves along axis An of link 5 which turns about fixed axis A. Centre 0 is placed at the centre of the ellipse and centre B at one of its foci. Then, when link 1 turns about axis 0, point D of slider 2 describes pedal curve q-q of the ellipse with respect to one of its vertices. The equation of pedal curve q-q is ρD=0͞D= a*cos(ϕ)+sqrt(a²-c²*sin²(ϕ)) or (x²+y²)²-2(x²+y²)ax=b²y² where ϕ is the polar angle between vector ρD and polar axis 0x.
$1178$LG,Ge$
|

 Click pentru a mări
Click pentru a mări






