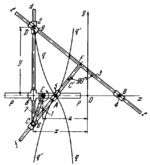
The lengths of the links comply with the conditions: E͞C=b, 0͞E=a, 0͞A=0͞B=sqrt(a²-b²) and a>b, where a and b are constant dimensions. Link 1, turning about fixed axis E, is connected by turning pair C to slider 6 which moves along stem Ff of T-shaped link 3. Cross-piece t-t of link 3 moves in sliders 4 and 9. Slider 4 turns about fixed axis B, and slider 9 is connected by turning pair D to slider 2. Slider 2 moves along axis Cd of link 7 which is connected by turning pair C to link 6. Link 7 is connected by a sliding pair to cross-shaped slider 8 which has guides perpendicular to each other. Slider 8 moves along fixed guides p-p whose axis coincides with axis 0x. When link 1 turns about axis E, point D of slider 2 describes cissoid of Steiner q-q with the equation y²[b²-(x-a)²]=[x²-(a²-b²)]². To trace symmetrical branch q'-q' of the cissoid of Steiner, link 1 and slider 6 should be rearranged so that point C is moved to point C', lying on stem Ff, and that distance E͞C' is equal to E͞C.
$1215$LG,Ge$