 Click pentru a mări Click pentru a mări
|
Description
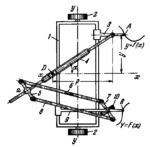
When stylus A is moved along curve y=f(x), carriage 1 travels along axis x-x on rollers 2. Slider 3 moves along the right-hand guide of carriage 1 in the direction of axis y-y. At this, slotted link 4 turns about pivot D which is fixed on the carriage. A parallel-crank linkage, consisting of links 5, 6, 7 and 8, moves along slotted link 4 by means of guide bushing a. Links 5 and 7 are perpendicular to link 4. Link 7 is connected by a turning pair to link 9 which slides along the left-hand guide of carriage 1. Wheel 10 is always parallel to slotted link 4 whose axis makes the angle α=arctan(f(x)/p) with the x-axis. Therefore, when stylus A is moved along curve y=f(x), f(x) wheel 10 describes a curve whose tangent is Y=(f(x)/p), and stylus B of integrating link 9 describes the integral curve Y=∫(tan(α)dx =∫(y/p)dx.
$1313$LG,MO$
|

 Click pentru a mări
Click pentru a mări






