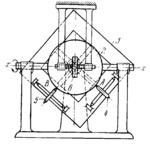
Ball 2 is driven by friction by wheel 6 and rotates about fixed axis x-x. Yoke 3 rotates about an axis passing through the centre of the ball and perpendicular to the plane of the drawing. Owing to friction, wheels 4 and 5 are rotated by ball 2. The angle of rotation of friction wheel 6 is proportional to the function y=f(α) being analyzed, and the motion of the ball is determined by the equation α₂=ρ₂y, where α₂ is the angle of rotation of the ball and ρ₂ is the proportionality factor. Without slip page at points A and B, yoke 3 is rotated an amount corresponding to qα. The angles of rotation of wheels 4 and 5 for q whole revolutions of the yoke are α₄-α₄₀=((R₂ρ₂)/R₄)*∫(sin(qα))dy=A_q; with limits [α=-π, α=π]; α₅-α₅₀=((R₂ρ₂)/R₅)*∫(cos(qα))dy=B_q; with limits [α=-π, α=π]; where A_q and B_q are the constant coefficients of a Fourier series for the given periodic function y=f(α), and R₂, R₄ and R₅ are the radii of ball 2 and wheels 4 and 5.
$3439$CF,MO$