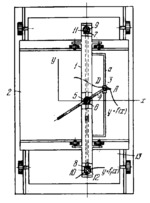
When tracing point A is moved along curve y=f(x), carriage 1 travels along axis x on fixed guide 2 and slider 3 travels on guide a along axis y. At the same time, sliding link 4 turns about axis D and slides in a slot of disk 5. When link 4 turns, disk 5 is turned with its rigidly attached bevel gear, also turning bevel gear 6 which is keyed to a shaft together with bevel gears 7 and 8. Rotation is transmitted from gears 7 and 8 to gears 9 and 10 to which wheels 11 and 12 with sharp-edged rims are attached (shown by dash lines). Thus, in any position, wheels 11 and 12 are always parallel to sliding link 4. Owing to friction, rotation of wheels 11 and 12 causes carriage 13 to move along axis y and the point of support (bearing) of wheel 12 to trace the integral curve y=(1/ρ)∫(f(x))dx=f₁(x). If the point of support of wheel 12 is moved along curve y=f₁(x), tracing point A traces the curve of the differential of the function.
$3442$CF,MO$