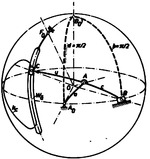
Ausgehend von der Euler-Savaryschen Gleichung der Kugelkinematik wurden die Krümmungen der Bahnkegel sphärischer Getriebe untersucht und Sonderfälle diskutiert. Die Frage nach den Bahnachsen mit vierach berührendem Krümmungskegel führt auf die sphärischen Analoga zur ... Kreisungs- und Angelpunktkurve. Sie sind Kegelflächen dritter Ordnung, die unter gewissen Voraussetzungen in solche niederer Ordnung zerfallen. Als Schnittgeraden des Kreisungskegels mit dem Wendekegel erhältman die Ballschen Achsen mit vierachsig berührender Tangentialebene. Auf dem Kreisungskegel kann es bis zu sechs reelle Achsen geben, die sogar einen fünfachsig berührenden Krümmungskegel besitzen. Die allgemein gültigen Ergebnisse über die Bahnkegel sphärisch bewegter Systeme lassen sich unter anderem auf die Koppelkegel sphärischer Gelenkgetriebe und Bahnkegel sphärischer Zykloiden anwenden. Es könnten daraus beispielsweise Rast- getriebe entwickelt werden.