 Click to enlarge Click to enlarge
|
Description
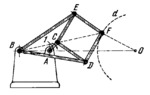
The lengths of the links comply with the conditions: C͞E=C͞D=D͞F=E͞F =a, B͞E=B͞D=b and A͞B >A͞C. The mechanism always satisfies the condition B͞C×B͞F=b²-a²=k² where k is the inversion constant. When crank 1 turns about fixed axis A, point F describes circle d which is the inversion of the circle described by point C. Centre 0 of the circle described by point F lies on the straight line passing through points B and A. Distances B͞A and B͞O are related by the condition B͞O=B͞A*(k²/(B͞A²-A͞C²)). Radius OF of the circle described by point F equals O͞F=A͞C(B͞O/B͞A). For the specified link length relationships, point F describes only a circular arc within the limits of the angle of turn of crank 1.
$704$LW,GI$
|

 Click to enlarge
Click to enlarge






