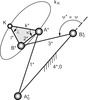
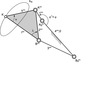
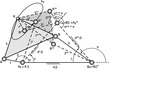
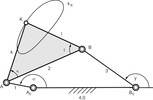
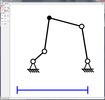
Modellgetriebe zum Satz von Roberts/Tschebyscheff

Getriebestruktur
Funktion	In der Praxis kommt es häufig vor, dass für eine vorgegebene Punktführungs-Aufgabe zwar ein viergliedriges Kurbelgetriebe mit vier Drehgelenken gefunden wurde, von dem ein Koppelpunkt K die gewünschte Koppelkurve k_K durchläuft, dass jedoch die übrigen Eigenschaften des Gelenkvierecks, wie die Abmessungen der Getriebeglieder, der Verlauf des Übertragungswinkels, die Lagen der Gestellpunkte oder der Platzbedarf, ungünstig sind. Mit Hilfe des Satzes von Roberts/ Tschebyschev über die dreifache Erzeugung von Koppelkurven kann man nun zu diesem vorher bestimmten Getriebe zwei weitere Gelenkvierecke ermitteln, die die gleiche Koppelkurve erzeugen, die aber aufgrund anderer Eigenschaften für den Anwendungsfall geeigneter sein können. Weitere Informationen zu diesem Getriebe finden sich in der Modellbeschreibung zum Satz von Roberts.
Getriebedimension	eben
Anzahl Getriebeglieder	4
Antriebsbewegung	Drehen
Abtriebsbewegung	Positionieren
Laufgrad	1
Enthaltene Grundgetriebe	Koppelgetriebe
Anzahl Antriebsglieder	1
Anzahl Abtriebsglieder	1
Umlauffähigkeit	ja
Umlauffähigkeit Antrieb	ja
Relativlage von An- und Abtriebsachse	parallel

Führungsaufgabe
Durchlaufsinn der Bahnkurve	gleichsinnig
Orientierung des Führungsgliedes	allgemein
Bahnkurve eines Gliedpunktes	geschlossen symmetrisch
Getriebedimension	eben
Antriebsbezug	möglich
Orientierungssinn des Führungsgliedes	schwingend: unbekannter Bereich

Anwendung
Anwendungsgebiete	Akademische Anwendung

Sammlungen

		Koppelgetriebe
		Akademische Anwendung
		Standmodelle aus Kunststoff

Permanentlinks

DMG-Lib		https://www.dmg-lib.org/dmglib/handler?mcdsc=197025
Europeana		http://www.europeana.eu/portal/record/2020801/dmglib_handler_mcdsc_197025.html